Power gear bug

The power gear bug expression refers, in the context of game mechanics investigations, to the underlying cause of the power gear effect. Power gear is one of the most remarkable bugs of Stunts, being in essence an overdrive mode available to some cars and reached under specific conditions that makes the car shoot to its overall top speed (limited only by the maximum rpm of the engine and gear ratio) and become essentially unaffected by grass slowdown. A proper explanation for the origins of power gear has eluded and frustrated custom car designers for a long time, as finding a consistent relation to usual performance parameters and the occurrence of power gear proved difficult. To complicate matters further, there are different kinds of power gear, with subtle differences between them, as well as anti-power gear, which causes a car to slow down in conditions that might otherwise trigger power gear. This article aims to present an unified theory for explaining both PG and anti-PG effect which proves useful for car tuners in practice.

PG classes

Stunts cars can be grouped into five classes with regard to their power gear behaviour, which are briefly defined below:

• Flexible PG cars - These cars can reach power gear as they move over most kinds of sloped surfaces (ramps, loops, etc.) and surface transitions as long as they do so above a certain critical speed. This speed depends on characteristics of the car (such as gear ratios, torque curve shape and aero drag) as well as on the inclination of the surface. In general, the critical speed drops as the acceleration of the car is reduced.
• Rigid PG cars - These cars can reach power gear exclusively by getting at or above the critical speed of 225mph as long as it does not have enough engine torque to keep accelerating on its own at such speeds (for conventional cars, that means their flat-track top speed must be below the critical speed). Surface characteristics do not affect the onset of rigid PG.
• Bug-free cars - These cars are completely free of the power gear bug. Additionally, they differ radically from conventional Stunts cars in that they are slowed down by aero drag whenever they reach speeds above the flat-track top speed via jump-boosting, thus displaying more reasonable physical behaviour.
• Regular cars - These cars also do not have neither PG nor anti-PG; however, they are able to conserve speeds higher than the flat-track top speed as long as the gas pedal is held (unlike true bug-free cars). At very high speeds (above 200mph) these cars may be subject to some speed loss when landing from jumps. The effect is, however, qualitatively different from, and much milder than, anti-PG.
• Anti-PG cars - These cars can be abruptly slowed down when driving through sloped surfaces or surface transitions if above some critical speed. Such critical speed depends on car and surface traits in essentially the same way observed for flexible PG cars.

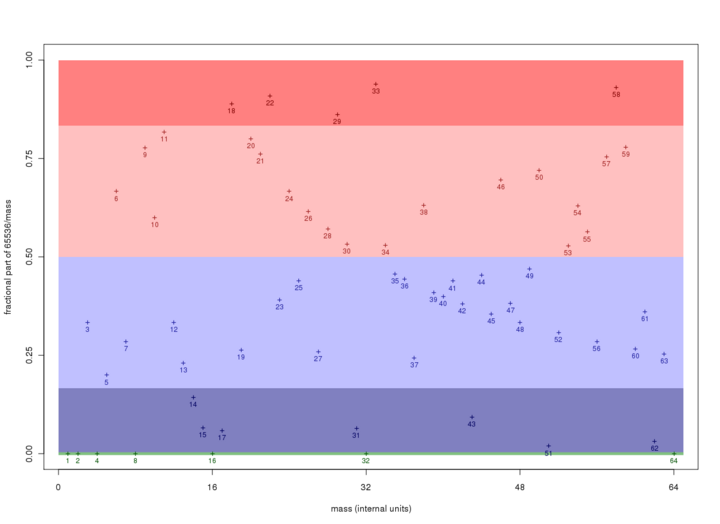
The magic formula

While the quantitative characteristics of the PG effect may depend on several other factors, the class to which a car belongs is exclusively determined by its mass. Letf be the fractional part (that is, the part of the number after the decimal point) of the quotient 65536/car_mass . The class of a car will then be determined by f through the following rule:

• f = 0 : Bug-free;
• 0 < f < 1/6 : Flexible PG;
• 1/6 < f < 1/2 : Rigid PG;
• 1/2 < f < 5/6 : Regular;
• 5/6 < f < 1 : Anti-PG.

It is important to emphasize the value of f does not influence the critical speeds for PG or anti-PG; thus, a car which belongs to one of the PG or anti-PG classes may be unable to reach the effect depending on other parameters - for instance, a rigid PG car which cannot reach 225mph at maximum rpm and highest gear due to its gear ratio settings will never reach PG.

A chart displaying the PG class (given by the coloured regions) for mass values from 1 to 64. Green (line): bug-free; dark blue: flexible PG; light blue: rigid PG; light red: regular; dark red: anti-PG.

Although the "magic" designation for the 65536/car_mass quotient seems appropriate at fist sight (as it seems to come out of nowhere), there is a reasonable hypothesis accounting for why the quotient is so important. The algorithm for determining speed increments per simulation frame must compute, directly or not, the ratio engine_force/car_mass . Available evidence strongly suggests that at some point of the calculation the result is determined as a 4-byte integer (instead of the regular 2-byte values used elsewhere) so that integer division by car_mass can be replaced by multiplication by 65536/car_mass with the aim of making the algorithm reasonably precise. The power gear bug most likely originates from improper handling of truncation errors in evaluating the quotient, leading to non-physical values for car acceleration.

Additional remarks

An approximate expression for the critical speed of flexible PG and and anti-PG cars is:

critical_speed = sqrt [2*(torque * gear_ratio - surface_constant)/aero_drag_constant]

In the above expression, the speed is in mph and all CAR*.RES parameters are given in internal units (that is, the values are taken as they are read from the file). The surface constant is a value that grows with the surface inclination; for common ramps it is approximately 200000 - and for loops (which get nearly vertical at places) it is expected to be much larger, lowering a lot the critical speed. The qualitative result given by the expression is that any parameter changes that lower car acceleration (other than increasing car mass) will reduce the critical speed. That's the reason why the Acura has lower critical speeds than Indy, for instance. The expression for critical speed ties three essential car features. That implies anyone interested in making a flexible PG or anti-PG car will have to design the car around the desired PG behaviour, potentially leading to lots of undesired compromises.

The PG classes for the original cars are (car masses are given in brackets):

• Flexible PG: Indy (15), Acura (31).
• Rigid PG: Ferrari (27), Corvette (35), Audi and Lancia (25, unreachable PG).
• Bug-free: Carrera (32)
• Regular: P962 (20), Jaguar (21), LM-002 (55)
• Anti-PG: Countach (33)

See also

• Car parameters
• Power Gear and Anti-Power Gear